Примеры решения задач по теме «Движение с постоянным ускорением»
- Подробности
- Обновлено 13.08.2018 21:12
- Просмотров: 949
«Физика — 10 класс»
Для решения задач по этой теме необходимо правильно записывать уравнение движения и уравнение зависимости скорости от времени.
Для некоторых задач разумно строить графики зависимости проекции скорости от времени и определять перемещение по графику, что часто удобнее, чем решать задачу аналитически.
Задача 1.
Ударом клюшки хоккейной шайбе сообщили скорость υ = 20 м/с. Через время t = 2 с скорость шайбы, движущейся прямолинейно, стала равна 16 м/с. Определите ускорение шайбы, считая его постоянным.
Р е ш е н и е.
Выберем оси координат так, чтобы движение шайбы происходило вдоль какой-нибудь координатной оси, например вдоль оси ОХ. За положительное направление оси ОХ примем направление вектора начальной скорости (рис. 1.47). Из определения ускорения следует: ах = (υ — υ)/t = -2 м/с2.
Знак «—» в конечном результате означает, что вектор ускорения направлен в сторону, противоположную положительному направлению оси ОХ. Модуль же ускорения а = |аx| = |-2 м/с2| = 2 м/с2.
Задача 2.
Перекрытие между первым и вторым этажами здания лифт проходил со скоростью υ = 4 м/с. Далее он начал тормозить и поднимался с постоянным ускорением а = 2 м/с2. Через время t = 2 с после начала торможения лифт остановился. Высота h каждого этажа равна 4 м. На какой высоте Н, считая от пола первого этажа, остановился лифт?
Р е ш е н и е.
Совместим начало координат с полом первого этажа и направим ось OY вертикально вверх. Так как ускорение лифта постоянно, то его движение будет описываться кинематическим уравнением у = у + υ0yt + ayt2/2.
Согласно условию задачи у = h, υ0y = υ, ау = -а, у = Н.
Поэтому Н = h + υt — at2/2; Н = 8м.
Задача 3.
На рисунке 1.48 изображена зависимость проекции скорости от времени.
1) Постройте графики зависимости ускорения и перемещения от времени.
2) Определите перемещение за время, равное t3.
3) Определите среднюю скорость движения за время, равное t3.
Р е ш е н и е.
В течение промежутка времени от 0 до материальная точка движется равноускоренно, так как скорость растёт со временем по линейному закону. Ускорение а1х = (υ1 — 0)/t1 = 1 м/с2.
В течение промежутка времени Δt — t2 — t1 материальная точка движется равномерно: υ = υ1 = const, а2 = 0. При t > t2 точка движется равнозамедленно с ускорением а3х = (0 — υ1)/(t3 — t2) = -0,5 м/с2.
На рисунке (1.49, а) изображён график зависимости аx от t. Зависимость x(t) в интервале 0 < t < t1 определяется по формуле х = 0 + a1xt2/2 и при t = t1, х1 = a1xt12/2 = 8 м. Скорость в момент времени t1 будет равна υ1, и тело начнёт двигаться равномерно:
х2 = х1 + υ1x(t2 — t1) = 32 м.
Начиная с t = t2 тело движется равнозамедленно:
x3 = x2 + υ1x(t3 — t2) — а3х(t3 — t2)2/2 = 48 м.
Средняя скорость движения
υср = x3/t3 ≈ 2,7 м/с.
График зависимости x(t) показан на рисунке (1.49, б). Кривая, изображающая зависимость x(t), состоит из трёх участков: параболы, прямой, параболы. Отметим, что парабола плавно переходит в прямую в точке А (и в точке В), так как значение мгновенной скорости определяется тангенсом угла наклона касательной к графику x(t) и в каждой точке графика должна быть единственная касательная. Перемещение также можно определить как площадь трапеции (см. рис. 1.48):
υ3 = υ1xt1/2 + υ1x(t2 — t1) + υ1x(t3 — t2)/2 = 48 м.
Следующая страница «Движение с постоянным ускорением свободного падения»
Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»
Кинематика — Физика, учебник для 10 класса — Класс!ная физика
Физика и познание мира —
Что такое механика —
Механическое движение. Система отсчёта —
Способы описания движения —
Траектория. Путь. Перемещение —
Равномерное прямолинейное движение. Скорость. Уравнение движения —
Примеры решения задач по теме «Равномерное прямолинейное движение» —
Сложение скоростей —
Примеры решения задач по теме «Сложение скоростей» —
Мгновенная и средняя скорости —
Ускорение —
Движение с постоянным ускорением —
Определение кинематических характеристик движения с помощью графиков —
Примеры решения задач по теме «Движение с постоянным ускорением» —
Движение с постоянным ускорением свободного падения —
Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» —
Равномерное движение точки по окружности —
Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение —
Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями —
Примеры решения задач по теме «Кинематика твёрдого тела»
Задачи на скорость сближения
Скорость сближения — это скорость, с которой объекты сближаются друг с другом.
Чтобы найти скорость сближения двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача 1. Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?

Решение: Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на:
40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:
60 — 40 = 20 (км/ч) — это скорость сближения автомобилей.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:
160 : 20 = 8 (ч).
Решение задачи по действиям можно записать так:
1) 40 · 4 = 160 (км) — расстояние между автомобилями,
2) 60 — 40 = 20 (км/ч) — скорость сближения автомобилей,
3) 160 : 20 = 8 (ч).
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 2. Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
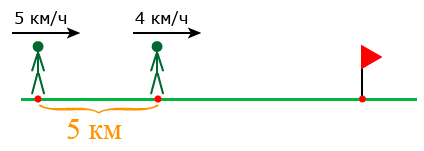
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:
5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:
5 : 1 = 5 (ч).
Решение задачи по действиям можно записать так:
1) 5 — 4 = 1 (км/ч) — это скорость сближения пешеходов,
2) 5 : 1 = 5 (ч).
Ответ: Через 5 часов второй пешеход догонит первого.






























