Решение ОГЭ 2021 Ященко Вариант №5 математика
Решение заданий варианта №5 из сборника ОГЭ 2021 по математике И.В. Ященко. ГДЗ для 9 класса.
ЧАСТЬ 1
Задание 1-5. Миша летом отдыхает у дедушки и бабушки в деревне Николаевке. Миша с дедушкой собираются съездить на велосипедах в село Игнатьево на железнодорожную станцию. Из Николаевки в Игнатьево можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Свистуху до деревни Берёзовки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Игнатьево. Есть и третий маршрут: в Свистухе можно свернуть на прямую тропинку, которая идёт мимо пруда прямо в Игнатьево. По шоссе Миша с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Николаевки до Свистухи равно 16 км, от Николаевки до Берёзовки – 36 км, а от Берёзовки до Игнатьево 15 км.
Задание 6. Найдите значение выражения 3,2 – 3,5·6,4
Задание 7. Одно из чисел , , , отмечено на прямой точкой.
alt=»Одно из чисел отмечено на прямой точкой. Какое это число?» width=»700″ height=»63″ /> Какое это число?
1) 2) 3) 4)
Задание 8. Найдите значение выражения при р = 5 и q = 2.
Задание 9. Решите уравнение x 2 + 8x + 15 = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Задание 10. В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Задание 11. Установите соответствие между формулами, которыми заданы функции, и графиками этих функций.
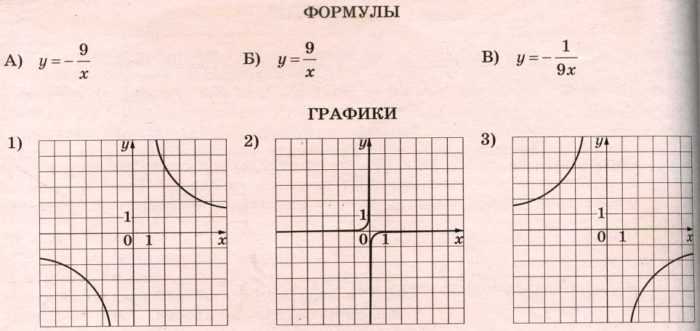
В таблице под каждой буквой укажите соответствующий номер.
Задание 12. Закон Джоуля – Ленца можно записать в виде , где Q – количество теплоты (в джоулях), I – сила тока (в амперах), R – сопротивление цепи (в омах), а t – время (в секундах). Пользуясь этой формулой, найдите сопротивление цепи R (в омах), если Q = 1296 Дж, I = 9 А, t = 2 c.
Задание 13. Укажите решение неравенства (x + 2)(х – 10) > 0.
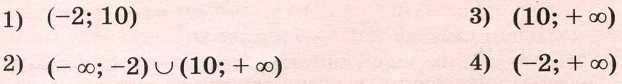
Задание 14. В амфитеатре 20 рядов. В первом ряду 56 мест, а в каждом следующем – на 2 места меньше, чем в предыдущем. Сколько всего мест в амфитеатре?
alt=»Решение ОГЭ 2021 Ященко Вариант №5 математика» width=»700″ height=»47″ /> Задание 15. Точки М и N являются серединами сторон АВ и ВС треугольника АBС соответственно. Отрезки АN и СМ пересекаются в точке О, АN = 18, СМ = 21. Найдите ОМ.
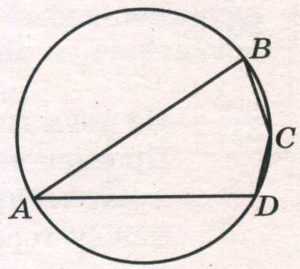
Задание 16. Угол А четырёхугольника АВСD, вписанного в окружность, равен 33°. Найдите угол С этого четырёхугольника. Ответ дайте в градусах.
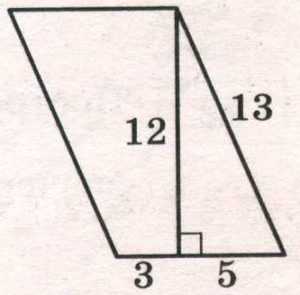
Задание 17. Найдите площадь параллелограмма, изображённого на рисунке.
Задание 18. На клетчатой бумаге с размером клетки 1 х 1 изображён ромб. Найдите длину его меньшей диагонали.
Задание 19. Какое из следующих утверждений не верно?
1) Через заданную точку плоскости можно провести только одну прямую. 2) Все равносторонние треугольники подобны. 3) Сумма острых углов прямоугольного треугольника равна 90 градусам.
В ответ запишите номер выбранного утверждения.
ЧАСТЬ 2
Задание 20. Решите неравенство
Задание 21. Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 51 минуту, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 251 км, скорость первого велосипедиста равна 10 км/ч, скорость второго – 20 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Задание 22. Постройте график функции и определите, при каких значениях m прямая у = m имеет с графиком ровно одну общую точку.
alt=»Решение ОГЭ 2021 Ященко Вариант №5 математика» width=»700″ height=»47″ /> Задание 23. Окружность пересекает стороны АВ и АС треугольника АВС в точках К и Р соответственно и проходит через вершины В и С. Найдите длину отрезка КР, если АР = 34, а сторона ВС в 2 раза меньше стороны АВ.
Задание 24. В треугольнике АВС с тупым углом АВС проведены высоты АА1 и CC1. Докажите, что треугольники А1ВС1 и АВС подобны.
Задание 25. В параллелограмме АВСD проведена диагональ АС. Точка O является центром окружности, вписанной в треугольник АВС. Расстояния от точки O до точки А и прямых АD и АС соответственно равны 25, 15 и 7. Найдите площадь параллелограмма АВСD.
Источник варианта: Сборник ОГЭ 2021 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.
Задание 1.
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.
Решение. Сначала идёт вводная часть, по сути, первое значимое предложение: «На первом этаже гостиная – самая большая по площади комната». Смотрим на рисунок, сразу видно, что самая большая комната на первом этаже – (3). Значит, (3) – гостиная. Подпишем её на рисунке. Кухня – тоже на первом этаже, вытянутая, длина в 2 раза больше ширины – это (1). Подпишем на рисунке: (1) – кухня.
Рядом с гостиной (3) находится столовая – это (2). Укажем её на рисунке. С первым этажом разобрались, «поднимаемся» на второй!
Комната Кости – над кухней. Значит, комната Кости – (7). Она соседняя с комнатой Вики – следовательно, комната Вики обозначена (6).
Комната родителей над столовой. Столовая – это (2). Над (2) находится (4). Она и есть комната родителей. Рядом с ней кабинет. Значит, кабинет – (5) .
Теперь на рисунке подписаны все комнаты. Заполняем таблицу. Переносим в бланк ответов по порядку цифры: 3751 . Это ответ к заданию 1.
Решений заданий 1-5 ОГЭ по математике
В ОГЭ по математике с 2020 года добавили новую линейку задач (1—5). Часть учеников пребывает в шоке от того, с чем им предстоит столкнуться на экзамене. Давайте разберёмся, так ли страшен чёрт, как его малюют.
Первое что пугает – это большое количество текста в условии. Факт. Но текст этот без формул и читается почти так же легко, как художественная литература. Давайте разберём на примере.
Задание 1.
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.
Решение. Сначала идёт вводная часть, по сути, первое значимое предложение: «На первом этаже гостиная – самая большая по площади комната». Смотрим на рисунок, сразу видно, что самая большая комната на первом этаже – (3). Значит, (3) – гостиная. Подпишем её на рисунке. Кухня – тоже на первом этаже, вытянутая, длина в 2 раза больше ширины – это (1). Подпишем на рисунке: (1) – кухня.
Рядом с гостиной (3) находится столовая – это (2). Укажем её на рисунке. С первым этажом разобрались, «поднимаемся» на второй!
Комната Кости – над кухней. Значит, комната Кости – (7). Она соседняя с комнатой Вики – следовательно, комната Вики обозначена (6).
Комната родителей над столовой. Столовая – это (2). Над (2) находится (4). Она и есть комната родителей. Рядом с ней кабинет. Значит, кабинет – (5) .
Теперь на рисунке подписаны все комнаты. Заполняем таблицу. Переносим в бланк ответов по порядку цифры: 3751 . Это ответ к заданию 1.
Задание 2.
На втором этаже расположен открытый балкон. На его бортике закреплены деревянные поручни. Определите их общую протяжённость (в метрах).
Решение. Бортик балкона находится по его периметру, кроме той части, которая примыкает к зданию. Его длина 11 м (считаем по сторонам клеток).
Задание 3.
Найдите площадь комнаты Вики. Ответ дайте в квадратных метрах.
Решение. Комната Вики уже подписана – это (6). Она состоит из 18 клеточек. Одна клетка соответствует квадрату 1 м на 1 м, то есть площадь одной клетки – 1 м². Площадь комнаты Вики – 18 м². Ответ: 18.
Задание 4.
В каждой из пронумерованных комнат, кроме Костиной, два окна, а в Костиной – всего одно. Других окон нет. Площадь стекла для каждого окна составляет 3 м². Стоимость окон при установке складывалась из стоимости стекла (3000 рублей за квадратный метр окна) и стоимости монтажа и фурнитуры (7000 рублей за каждое окно). Определите общую стоимость всех окон и их установки. Ответ дайте в рублях.
Решение. Пронумерованных комнат 7, в 6 из них по два окна (это уже 12 окон), в одной комнате – 1 окно. Всего 12 + 1 = 13 окон. Посчитаем стоимость одного окна. 3 м² стекла стоят 3*3000=9000 рублей, монтаж и фурнитура – 7000 рублей. Общая стоимость одного окна равна 9000+7000 = 16000 рублей. Стоимость всех окон равна 13*16 000 = 208000 рублей. Ответ: 208000.
Задание 5.
После постройки дома денег на внутреннюю отделку осталось меньше, чем планировалось первоначально, поэтому пришлось экономить.
В гостиной и столовой предполагалось класть паркетную доску, но обошлись ламинатом, а на сэкономленные деньги приобрели туристические путёвки в Крым. Ламинат и паркетная доска продаются только в упаковках. Каждая упаковка содержит одинаковое число квадратных метров материала.

